Are you ready to dive into the world of efficient array manipulation? Today, let's talk about the Two Pointer Approach - a powerful technique used to solve various array problems.
Before Deep Dive into Advance: Let's once again dig into basic programming
Problem : Find the second maximum element in the array.
Pseudo Code :
It initializes two variables, `largest` and `secLargest`, to the smallest possible integer value (i.e. Integer.MIN_VALUE).
It iterates through the array, updating `largest` and `secLargest` as it finds larger elements.
If an element is larger than the current largest, it updates `secLargest` to the previous largest value and updates largest to the new element.
If an element is larger than `secLargest` but not equal to `largest`, it updates `secLargest` to the new element.
Finally, it returns the value of `secLargest`, which is the second largest element in the array.
public class SecondMaxElement { public static int findSecondLargest(int[] arr) { int largest = Integer.MIN_VALUE; int secLargest = Integer.MIN_VALUE; for(int i =0; i < arr.length; i++ ) { if(arr[i] > largest) { secLargest = largest; largest = arr[i]; }else if(arr[i] > secLargest && arr[i]!= largest) { secLargest = arr[i]; } } return secLargest; } public static void main(String[] args) { int[] myArr = {1,4,25,9,25,13,24,29}; int result = findSecondLargest(myArr); System.out.println("Second Largest in the array : "+ result); } }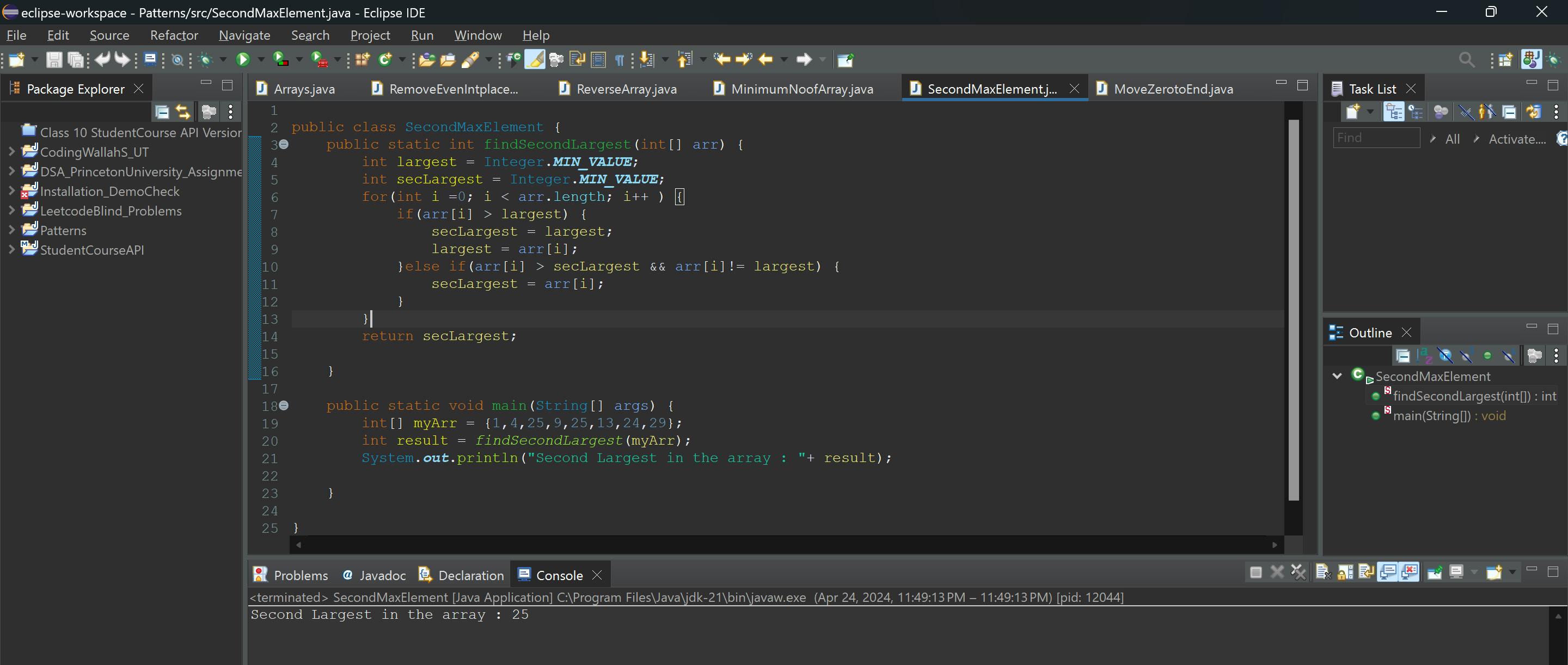
🚀 Now let's exploring the Two Pointer Approach in Arrays 🌟
What exactly is the Two pointer approach?
The Two Pointer Approach is a technique used in algorithms where two pointers iterate through an array simultaneously. These pointers move at different speeds or start from different positions, allowing efficient traversal and manipulation of the array.
Advantages of the Two Pointer Approach:
Optimized Time Complexity: By traversing the array only once or with minimal iterations, the Two Pointer Approach often results in better time complexity compared to brute-force solutions.
Reduced Space Complexity: Unlike some other algorithms, this approach requires minimal extra space, making it memory-efficient.
Solves Multiple Problems: The Two Pointer Approach is versatile and can be applied to a wide range of problems, including those involving sorting, searching, and manipulation.
Problem: Move the zero’s to the end of array by making sure that the elements are in relative order.
Pseudo Code:
Initialize two pointers, 'i' and 'j', where 'i' iterates through the array and 'j' tracks the position to place zeros.
Iterate through the array.
If the current element is not zero and the element at position 'j' is zero (arr[i] != 0 && arr[j] == 0), swap arr[i] and arr[j]).
Ensure to increment 'j' if arr[j] is not zero.
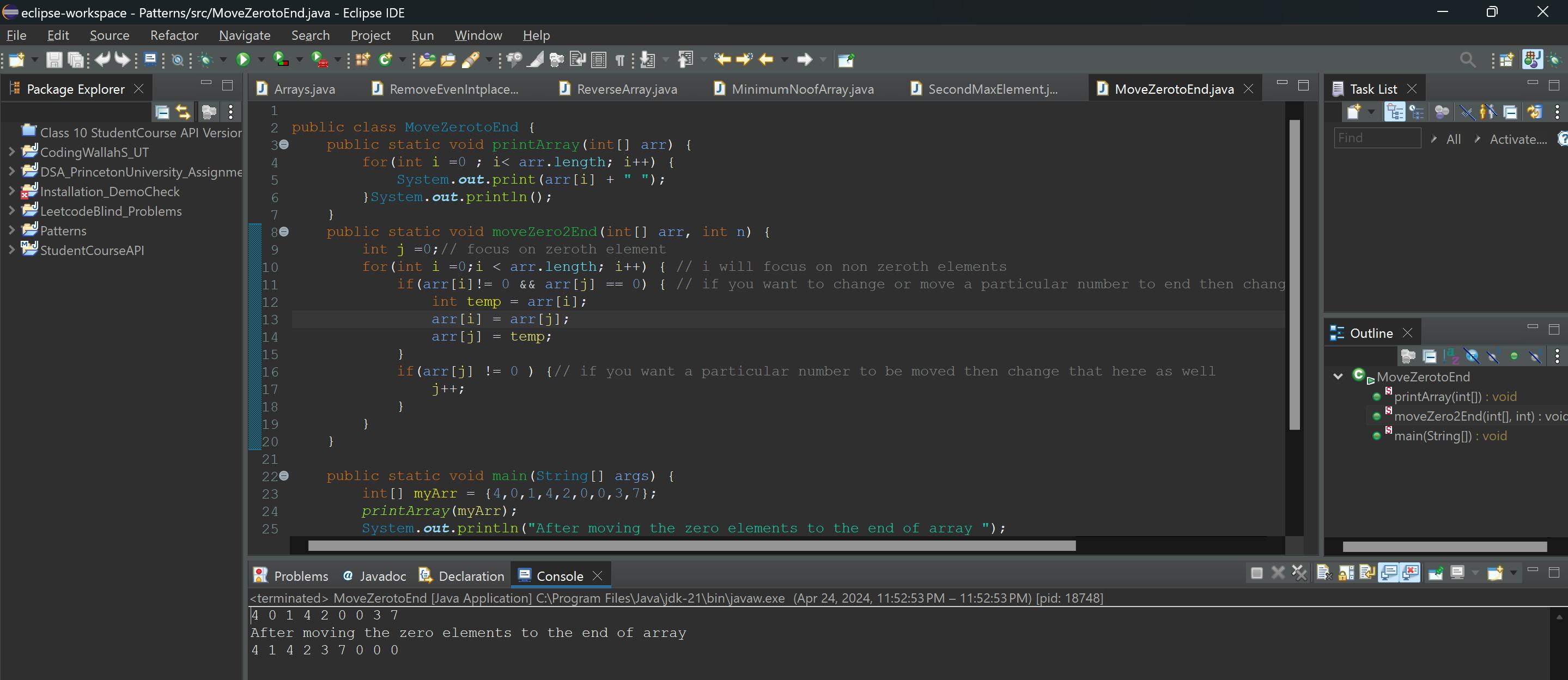
public class MoveZerotoEnd { public static void printArray(int[] arr) { for(int i =0 ; i< arr.length; i++) { System.out.print(arr[i] + " "); }System.out.println(); } public static void moveZero2End(int[] arr, int n) { int j =0;// focus on zeroth element for(int i =0;i < arr.length; i++) { // i will focus on non zeroth elements if(arr[i]!= 0 && arr[j] == 0) { // if you want to change or move a particular number to end then change that in this statement i,j int temp = arr[i]; arr[i] = arr[j]; arr[j] = temp; } if(arr[j] != 0 ) {// if you want a particular number to be moved then change that here as well j++; } } } public static void main(String[] args) { int[] myArr = {4,0,1,4,2,0,0,3,7}; printArray(myArr); System.out.println("After moving the zero elements to the end of array "); moveZero2End(myArr , myArr.length); printArray(myArr); } }
How to resize an array in java
In Java, resizing an array involves creating a new array with a larger size and copying elements from the old array to the new one. While there isn't a built-in method to resize arrays directly, the Arrays.copyOf() method from the java.util package can be used to resize arrays efficiently.
Here's a concise guide on how to resize an array in Java:
Determine the new size for the array.
Use the Arrays.copyOf() method to create a new array with the desired size.
Copy elements from the old array to the new one.
Update references to the old array with the new array.
// How internally resizing will be done. Assume as below
Public void resize(int[] arr, int int capacity){
Int[] temp = new int[capacity];
For(int i=0; i< arr.length; i++){
Temp[i] = arr[i];
}
arr =temp;
}
But even after you resize this with void as return it will get garbage collected later so you have to change the return type to int[] so that it will return the resized array.
Public int[] resize(int[] arr, int int capacity){
Int[] temp = new int[capacity];
For(int i=0; i< arr.length; i++){
Temp[i] = arr[i];
}
arr =temp;
return arr; // or else directly you can return the temp array as return temp without last two lines
}
🌟 Thank you all for reading! 📚✨
Your feedback is valuable to me! 🙏 If you have any suggestions or inputs to improve my articles or writing skills, please don't hesitate to comment below. Your input will help me level up and create better content in the future. 😊🚀